Actividad 1
Consideramos la experiencia aleatoria ''tirar una moneda común y observar la cara superior''.
- Escribe el espacio muestral de este experimento.
- Considerando como dominio de la probabilidad $\mathcal{A}=\{\Omega, \emptyset, \{\mbox{número}\}, \{\mbox{cara}\}\}$, asigna a cada elemento su probabilidad justificando. ¿Con que enfoque has asignado las probabilidades?
- ¿La función que armaste en la parte anterior es una probabilidad?, ¿cumple los axiomas?, justifica.
Actividad 2
Consideramos la experiencia aleatoria ''tirar una moneda cargada y observar la cara superior''
- Escribe el espacio muestral de este experimento.
- Considerando como dominio de la probabilidad $\mathcal{A}=\{\Omega, \emptyset, \{\mbox{número}\}, \{\mbox{cara}\}\}, si se ha tirado esta moneda una cantidad muy grande de veces y los resultados de la frecuencia relativa de cara de la moneda se muestran en el siguiente diagrama:
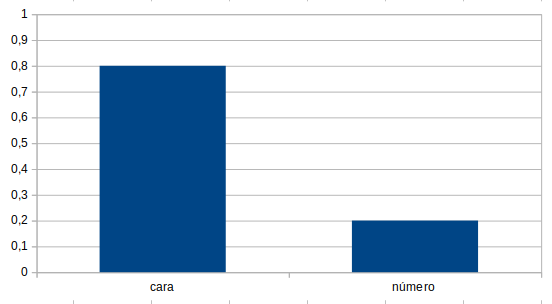
asigna a cada suceso su probabilidad justificando. ¿Con qué enfoque(es) has asignado las probabilidades?
3. Demuestra que la función que armaste en la parte anterior es una probabilidad (cumple con los axiomas)
Actividad 3
El espacio de probabilidades clásico o de Laplace
Supongamos que nuestro espacio muestral es finito, $\Omega =\left \{ w_1, w_2, ....,w_n \right \}$ y que $\mathcal{A} = \mathcal{P}(\Omega)$.
Definamos las siguientes probabilidades:
$P(\left \{ w_1\right \})=P(\left \{ w_2 \right \})=\cdots=P(\left \{w_n \right \})=\frac{1}{n}$.
Si $A$ es un suceso (en este caso un subconjunto cualquiera de $\Omega$), compuesto por $k$ sucesos elementales, entonces $A=\left \{ w_{i_1}, w_{i_2}, ....w_{i_k} \right \} = \bigcup_{j=1}^{k}\{w_{i_j}\}$.
- ¿Cómo definirías $P(A)$?
- Así definida, ¿se cumplen los axiomas de Kolmogorov?